分数的意义是几年级的内容_分数的意义

1.分数的意义和概念是什么？

2.分数的意义怎么写？

3.分数的意义是什么？

4.分数表示的意义是什么

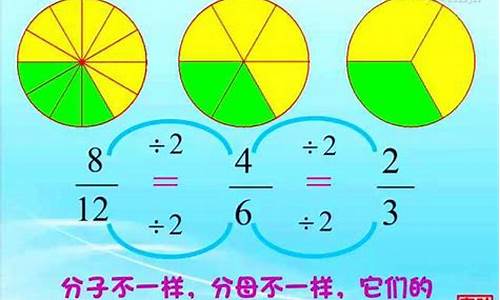
分数的意义是：一个物体，一个图形，一个计量单位，都可看作单位“1”。把单位“1”平均分成几份，表示这样一份或几份的数叫做分数。

在分数里，表示把单位“1”平均分成多少份的叫做分母，表示有这样多少份的叫做分子；其中的一份叫做分数单位。

注意事项

①分母一定不能为0，因为分母相当于除数。否则等式无法成立，分子可以等于0，因为分子相当于被除数。相当于0除以任何一个数，不论分母是多少，答案都是0。

②分数中的分子或分母经过约分后不能出现无理数（如2的平方根），否则就不是分数。

③一个最简分数的分母中只有2和5两个质因数就能化成有限小数；如果最简分数的分母中只含有2和5以外的质因数那么就能化成纯循环小数；如果最简分数的分母中既含有2或5两个质因数也含有2和5以外的质因数那么就能化成混循环小数。

分数的意义和概念是什么？

分数的三种意义如下：

分数的意义：把单位1平均分成若干份，表示这样一份或几份的数，叫做分数。分数原是指整体的一部分，或更一般地，任何数量相等的部分，表现形式为一个整数a和一个整数b的比。

分数表示一个数是另一个数的几分之几，或一个与所有的比例。把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。当分母为100的特殊情况时，可以写成百分数的形式，如1%。

真分数的意义：分子小于分母的分数叫做真分数，真分数＜1。（真分数的分子小于分母。）

分数的意义：分子大于或等于分母的分数叫分数，分数≥1，（分数的分子等于或大于分母）

带分数的意义：由整数部分和真分数部分组成的分数叫做带分数，带分数＞1，（写带分数时，先写整数部分，再写分数部分。）读带分数时，先读整数部分，再读分数部分，中间加一个又字。分数是指分子小于分母的分数，最简分数是指分子和分母互质的分数。

分数的特点

1、分子和分母：分数由分子和分母两部分组成，分子表示被分割的部分，分母表示总共分割成的部分。

2、分数线：分数线是分子和分母之间的横线，用于表示它们的比例关系。

3、真分数和分数：当分子小于分母时，分数被称为真分数；当分子大于或等于分母时，分数被称为分数。

4、约分：如果分子和分母有相同的因子，那么它们可以被约分，即分子和分母同时除以它们的最大公约数，得到一个等价的分数。

5、小数和百分数：分数可以转化为小数或百分数形式，小数形式是将分子除以分母得到的结果，百分数形式是将小数形式乘以100得到的结果。

分数的意义怎么写？

意义：将一个物体看成一个单位“1”，然后将整个单位“1”平均分成几份，其中表示这一份或者几份的数就可以称为“分数”，代表着这一份或几份在整个单位中的占比。

概念：把单位1平均分成若干份，表示这样的一份或几份的数叫分数。分数告诉我们分数的分子和分母要同时乘或除以相同的数时。

分数性质：

分数的性质与分数的计算息息相关，分数有一个有趣的性质：一个分数不是有限小数，就是无限循环小数，像π等这样的无限不循环小数，是不可能用分数代替的，这个性质决定了分数部分含义。

还有一个性质是当分子与分母同时乘或除以相同的数，分数值不会变化。因此，每一个分数都有无限个与其相等的分数。利用此性质，可进行约分与通分。分数通分需要根据分数的基本性质，把几个异分母分数化成与原来分数相等的同分母的分数。

分数的意义是什么？

（1）分数的意义。把单位“1”平均分成若干份，表示这样的一份或几份的数，叫做分数。

（2）单位“1”的含义。单位“1”不仅可以表示一个东西、一个计量单位、一条直线，也可以表示由一些物体组成的整体。如：一袋米、一个工厂、一车间工人等。

（3）分数单位的意义。把单位“1”平均分成若干份，表示这样的1份的数，叫做分数单位。

分数（来自拉丁语，“破碎”）代表整体的一部分，或更一般地，任何数量相等的部分。 当在日常英语中说话时，分数描述了一定大小的部分，例如半数，八分之五，四分之三。 分子和分母也用于不常见的分数，包括复合分数，复数分数和混合数字。

分数表示一个数是另一个数的几分之几，或一个与所有的比例。把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。分子在上，分母在下。

最早的分数是整数倒数：代表二分之一的古代符号，三分之一，四分之一，等等。埃及人使用埃及分数c。 1000 bc。大约4000年前，埃及人用分数略有不同的方法分开。他们使用最小公倍数与单位分数。他们的方法给出了与现代方法相同的答案。埃及人对于Akhmim木片和二代数学纸莎草的问题也有不同的表示法。

希腊人使用单位分数和（后）持续分数。希腊哲学家毕达哥拉斯（c。530 bc）的追随者发现，两个平方根不能表示为整数的一部分。 （通常这可能是错误的归因于Metapontum的Hippasus，据说他已被处决以揭示这一事实）。在印度的150名印度人中，耆那教数学家写了“Sthananga Sutra”，其中包含数字理论，算术学操作和操作。

现代的称为bhinnarasi的分数似乎起源于印度在Aryabhatta（c。ad 500），[引用需要] Brahmagupta（c。628）和Bhaskara（c。1150）的工作。他们的作品通过将分子（Sanskrit：amsa）放在分母（cheda）上，但没有它们之间的条纹，形成分数。在梵文文献中，分数总是表示为一个整数的加和减。整数被写在一行上，其分数在两行的下一行写成。如果分数用小圆?0was或交叉?+ was标记，则从整数中减去;如果没有这样的标志出现，就被理解为被添加。

分数表示的意义是什么

1

分数的意义：一个物体，一个图形，一个计量单位都可以看为一个单位“1”，将单位“1”平均分为几份后，表示这一份或者几份的数就可以称为“分数”，分数中，单位“1”被分成多少份的就是分母，有这样多少份就是分子；其中的一份叫做分数单位。

分数原是指整体的一部分，或更一般地，任何数量相等的部分。表现形式为一个整数a和一个整数b的比（a为b倍数的分数是否属于分数存在争议?）。分数表示一个数是另一个数的几分之几，或一个与所有的比例。把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。分子在上，分母在下。当分母为100的特殊情况时，可以写成百分数的形式，如1%。

分数在数的学习中占很重要的地方为，很多人不了解分数的意义，其实很简单，它的意义为：一个物体，一个图形，一个计量单位，都可看作单位“1”。把单位“1”平均分成几份，表示这样一份或几份的数叫做分数。在分数里，表示把单位“1”平均分成多少份的叫做分母，表示有这样多少份的叫做分子；其中的一份叫做分数单位。分子与分母同时乘或除以一个相同的数（0除外），分数的大小不变，这就是分数的基本性质。

分数中间的一条横线叫做分数线，分数线上面的数叫做分子，分数线下面的数叫做分母。读作几分之几。分数可以表述成一个除法算式：如二分之一等于1除以2。其中，1 分子等于被除数，－ 分数线等于除号，2 分母等于除数，而0.5分数值则等于商。分数还可以表述为一个比，例如；二分之一等于1：2，其中1分子等于前项，—分数线等于比号，2分母等于后项，而0.5分数值则等于比值。

分数还有一个有趣的性质：一个分数不是有限小数，就是无限循环小数，像π等这样的无限不循环小数，是不可能用分数代替的。分数的另一个性质是：当分子与分母同时乘或除以相同的数（0除外），分数值不会变化。因此，每一个分数都有无限个与其相等的分数。利用此性质，可进行约分与通分。

分数的意义如下：

把单位1平均分成若干份，表示这样一份或几份的数，叫做分数。分数原是指整体的一部分，或更一般地，任何数量相等的部分，表现形式为一个整数a和一个整数b的比。

分数表示一个数是另一个数的几分之几，或一个与所有的比例。把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。当分母为100的特殊情况时，可以写成百分数的形式，如1%。

真分数的意义:分子小于分母的分数叫做真分数，真分数＜1。（真分数的分子小于分母。）

分数的意义：分子大于或等于分母的分数叫分数，分数≥1，（分数的分子等于或大于分母）

带分数的意义：由整数部分和真分数部分组成的分数叫做带分数，带分数＞1，（写带分数时，先写整数部分，再写分数部分。）读带分数时，先读整数部分，再读分数部分，中间加一个“又”字。分数是指分子小于分母的分数，最简分数是指分子和分母互质的分数。

历史

最早的分数是整数倒数：代表二分之一的古代符号，三分之一、四分之一等等。埃及人使用埃及分数c。1000bc。大约4000年前，埃及人用分数略有不同的方法分开。他们使用最小公倍数与单位分数。他们的方法给出了与现代方法相同的答案。埃及人对于Akhmim木片和二代数学纸莎草的问题也有不同的表示法。

希腊人使用单位分数和（后）持续分数。希腊哲学家毕达哥拉斯（c。530bc）的追随者发现，两个平方根不能表示为整数的一部分。。在印度的150名印度人中，耆那教数学家写了“Sthananga Sutra”，其中包含数字理论，算术学操作和操作。